撰文:ck.eth
編譯:Lylia
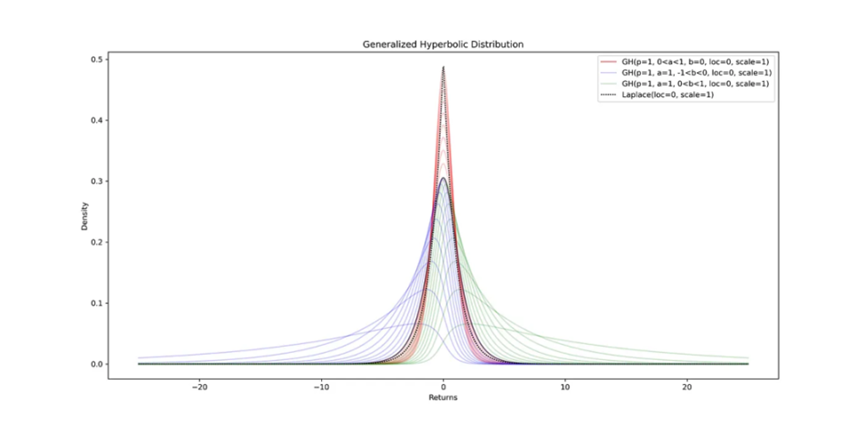
雙曲分佈[1],最初是為了模擬風沙波動[2](沙漠中的沙子動態)而開發的,由於其參數的靈活性[3], 在建模金融資產回報方面具有應用。
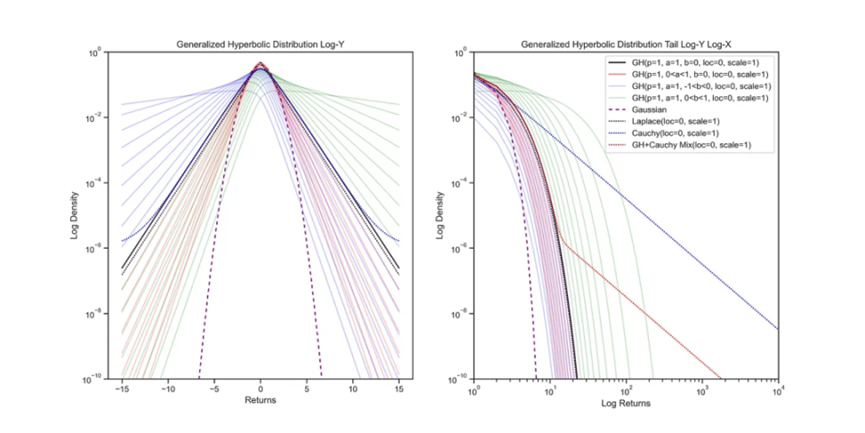
左圖:在對數 – 縱坐標圖上觀察統計分佈可以更好地瞭解其形狀。超博拉分佈呈現出類似於雙曲線的形狀,而虛線高斯分佈由於 e^-x²/2 項的存在可以看作是一個抛物線。右圖:透過在對數 – 對數圖上觀察分佈的尾部,可以更好地瞭解其特徵。冪律分佈在對數 – 對數圖中不會呈現出衰減的趨勢。可以透過將分佈組合並使用權重參數來混合不同的分佈。
數位資產的價格行為
對於流動性提供者(LP)來說,瞭解自己資產的價格動態是非常有用的。如果我們在以對數 – 縱坐標圖的形式觀察自 2015 年以來最古老的數位資產比特幣(BTC)的歷史資料,使用了 3091 個每日收益率資料,我們會發現除了一些離群值,廣義雙曲線分佈在歷史上可以很好地擬合每日收益率。
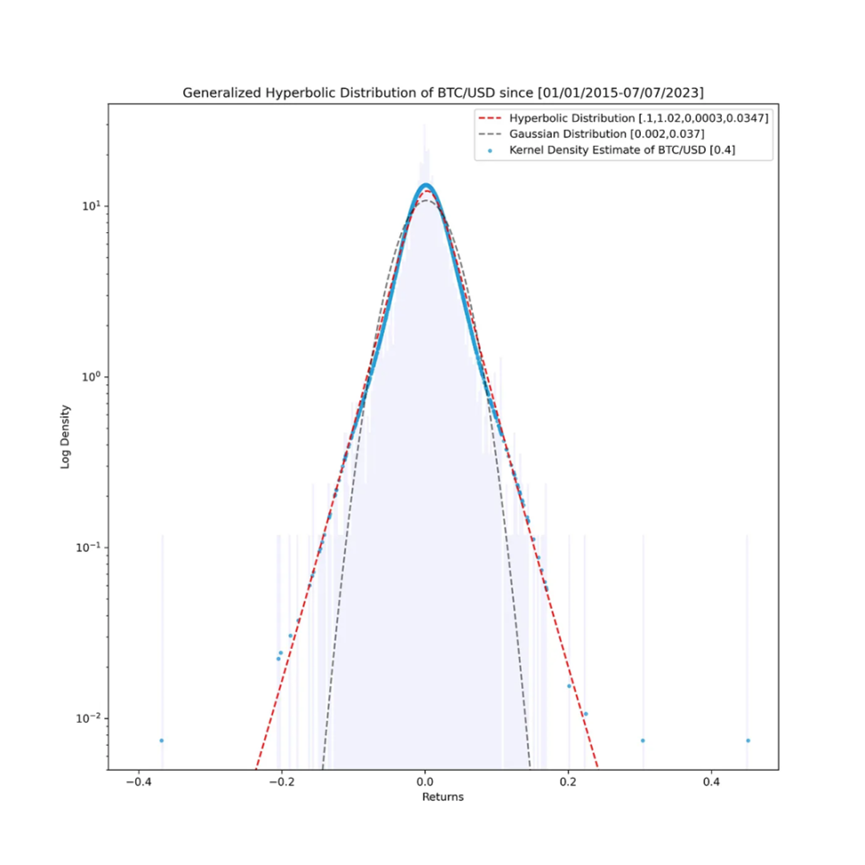
我們的擬合異常之處恰好是位於最右側和最左側的離群值,在對數 – 對數圖中可以觀察到這些值。在該圖中,我們可以看到負收益率的尾部用紅色表示,而正的離群收益率用藍色表示。
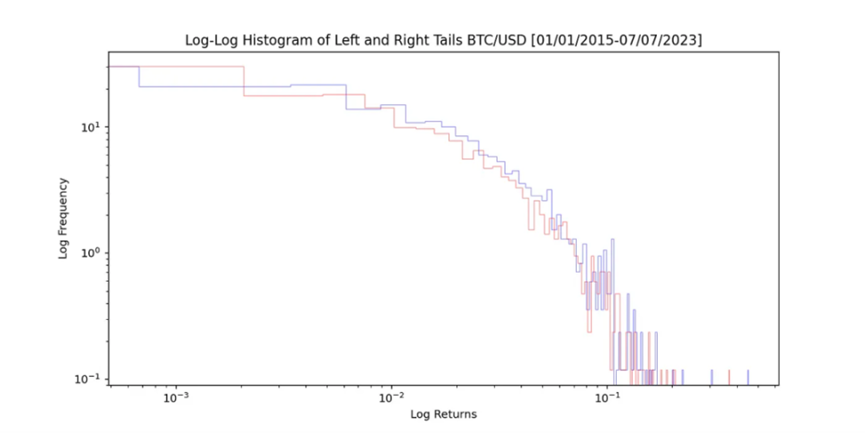
儘管尾部看起來相似,但右側的離群值存在一些不匹配。為了平滑長條圖,我使用了核密度估計(KDE)方法。
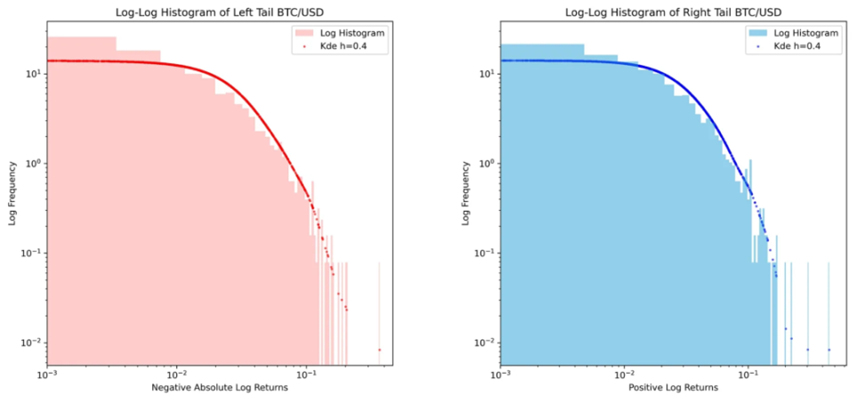
自 2015 年 1 月 1 日起,比特幣(BTC)每日收益率的左尾和右尾顯示出不對稱性,尤其是右尾。
這意味著將廣義雙曲線與非對稱冪律結合起來可以描述比特幣價格的動態。需要注意的是,我選擇比特幣作為示例,因為它是最古老的時間序列,同時也是所有數位資產中最不易波動的,這意味著其他數位資產的流動性提供者(LPs)將表現出更加波動的行為。
價格動態建模
有數十種統計分佈可以混合使用,以模擬這種波動行為。例如,在傳統金融領域中,一種常用的方法是使用幾何布朗運動(對數正態分佈)並將其與勒維過程(泊松分佈)相結合,以考慮價格的跳躍。
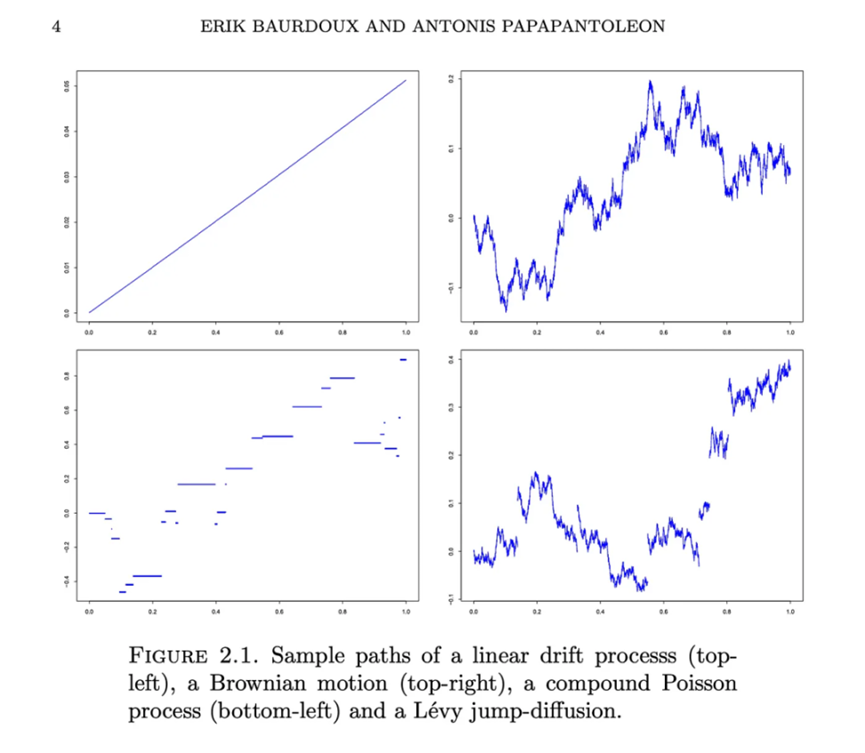
由 Erik Bardoux 和 Antonis Papapantoleon 在關於勒維過程的講座中視覺化的類比路徑。
我在 Desmos 上創建了一個包含 50 多種統計分佈的庫,以幫助用戶探索這些分佈以及如何透過 Riemann 積分在 Uniswap 上複製這些分佈的 LP 頭寸。
統計分佈庫的 Desmos 連結:https://www.desmos.com/calculator/4ey6hbevzf
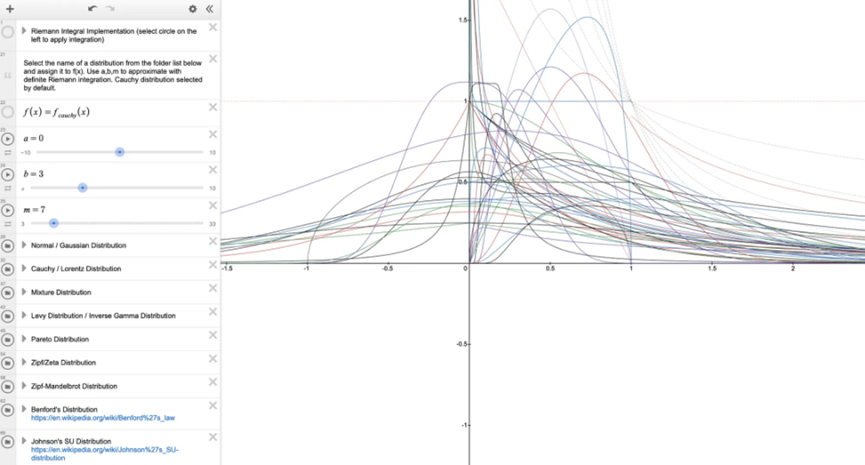
Desmos 的一個有趣特點是可以切換到對數對數圖,這樣可以看到每個統計分佈的尾部特徵是如何變化的。
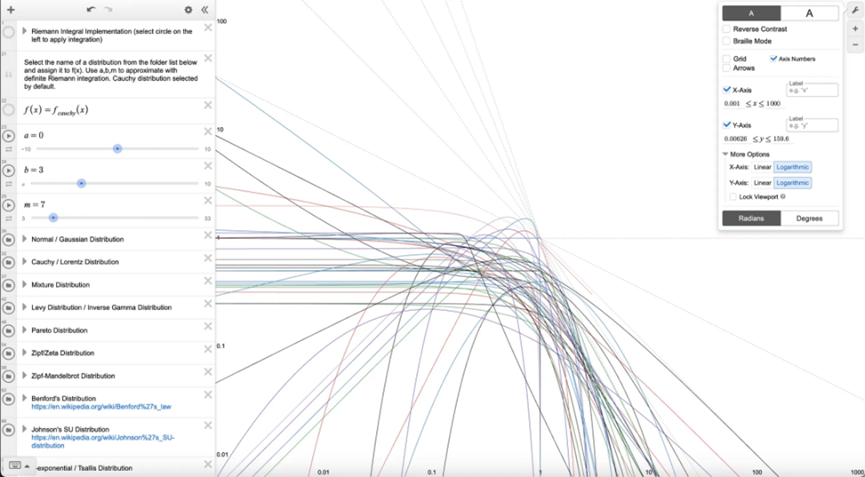
如果想要比較哪種分佈最適合自己的資料,可以使用 Kolmogorov-Smirnov 檢驗將累積分佈函數與經驗累積長條圖資料進行比較。但是,我們也可以使用下面的一種簡單方法,只需假設可能最糟糕的分佈。
如果對未來的情況一無所知,怎麼辦呢?嗯,我們可以思考在價格空間中最差的可能分佈是什麼樣的,即其尾部呈現無限延伸的冪律。其中一種分佈就是柯西分佈(在價格空間中,對應的是對數柯西分佈)。
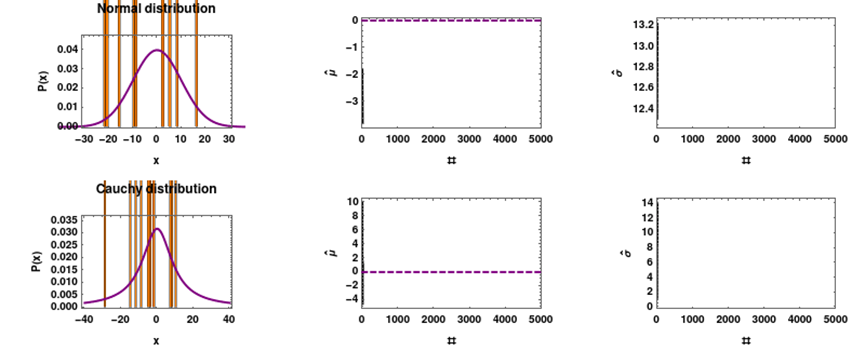
柯西分佈不遵循大數定律,它擁有自己的意願。你可以參考這個連結:https://en.wikipedia.org/wiki/Cauchy_distribution#/media/File:Mean_estimator_consistency.gif,瞭解柯西分佈的特性。
柯西分佈的一個特性是它不符合大數定律。你可能會計算過去 30 天的平均值,以為你看到了一種模式,但實際上它可能欺騙你。一個有趣的例子是 DOGE/ETH 交易對的平均值,由於缺乏流動性,它可能表現出這種行為。
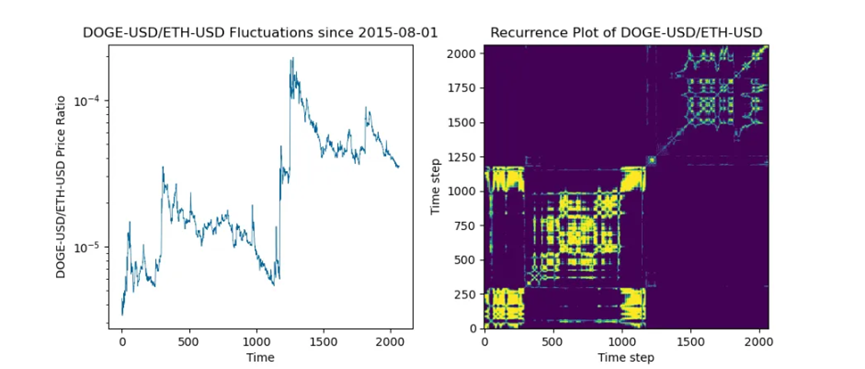
儘管 Dogecoin 和 Ethereum 已經存在了 7 年以上,但這對交易對的跳躍過程卻有自己的特點,這使得應用統計近似方法變得困難。
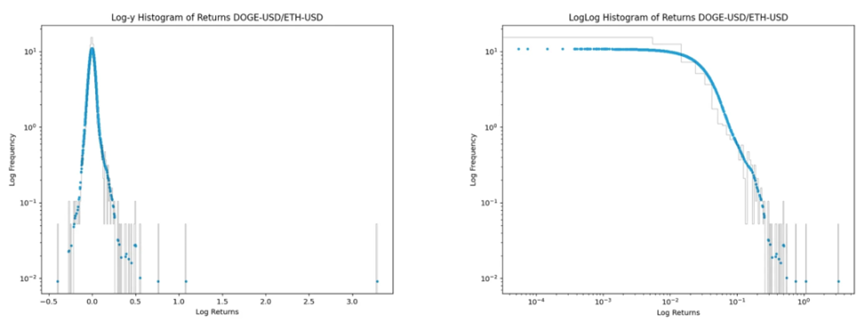
右側的 loglog 長條圖中存在逐漸成長的離群值。我瞭解到,在 loglog 圖中具有逐漸成長離群值的分佈是對數柯西分佈。
我們可以看到柯西分佈在價格空間中相對於對數正態分佈的樣子。
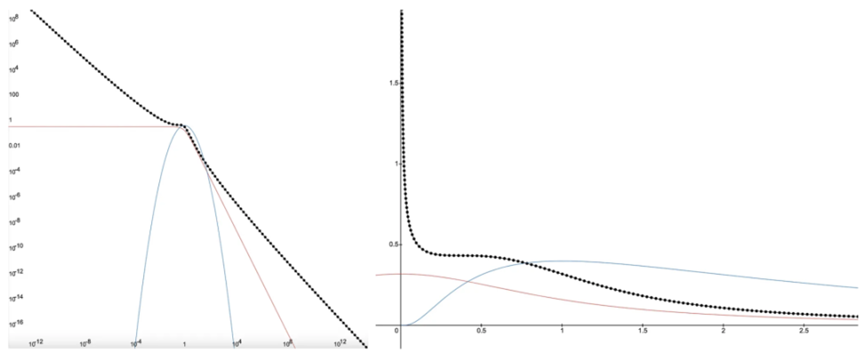
左側: 對數正態分佈的 loglog 圖形呈抛物線狀,紅色表示柯西冪律的線性尾部,黑色虛線表示對數柯西分佈 右側: 同樣的分佈在價格空間中的表示,範圍從[0,無窮大 )。
對數柯西分佈並不像完全範圍的 Uniswap v2 倉位那樣糟糕,但它是第二糟糕的情況。根據我們在第 1 和第 2 部分對於資本效率優化的知識,將下限設定在 80-90% 左右可以幫助改善它,因為隨著價格接近下限,分佈開始成長,因此不需要一直提供流動性直至零。
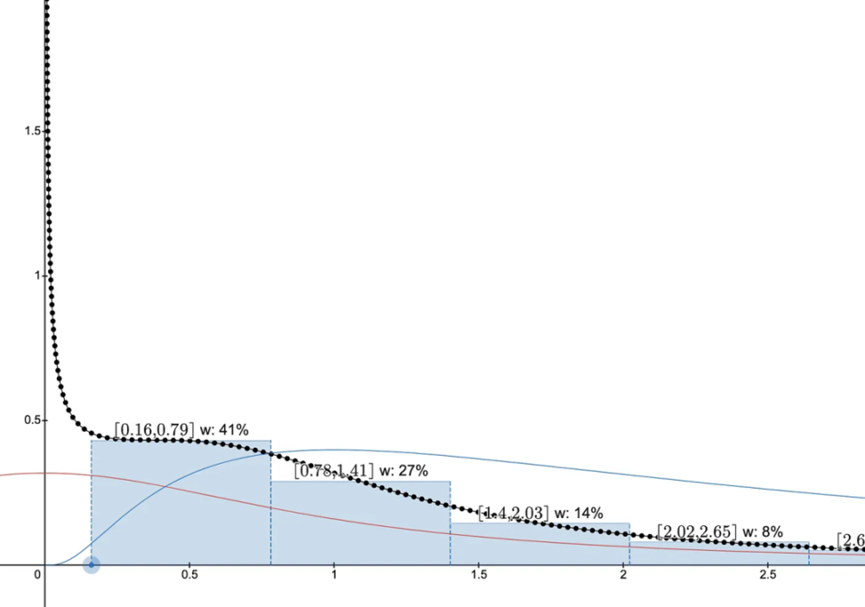
從當前價格 1 開始,將下限設定為 80-90% 可以作為限制範圍的起點,但我不建議根據這樣的動態來投資 / 購買 / 出售任何資產,這並不是金融建議。最佳做法是等待並更多地瞭解一種資產。
關於複雜系統中的冪律分佈
但是,像柯西分佈這樣的冪律分佈會隨著時間的推移變得尾部較短嗎?在像加密貨幣這樣不斷演化的複雜系統中,很難完全消除冪律現象(參見附錄),但可以減少不確定性的程度。
仔細思考一下,所有資產在初始階段都曾經歷過不確定性的時刻。事實上,隨著自動化做市商(AMM)的發展,我們發現了傳統金融市場上無法預測的有趣聯繫。人們使用平方根定律來統計估計價格影響。透過 AMM,我們可以準確預測價格僅僅作為集中流動性的函數而受到的影響,並且無需考慮交易量或波動率來定義某個時刻的價格影響。將論點推向極端,假設 Jerome Powell 下載了 MetaMask,並決定在 DOGE/ETH 中提供流動性資金,並提供數萬億美元的流動性。每個試圖出售 DOGE 的人對價格的負面影響幾乎可以忽略不計,從返回分佈中可以看到,隨著時間的推移,波動性會下降,逐漸變得不太像柯西分佈。
因此,有一個有足夠資金的流動性供應商勇敢大膽地在長時間內為 AMM 提供過多流動性,就有可能降低資產的波動性。雖然我懷疑很少有人能夠在手邊有一個數字貨幣印表機來增加他們的勇氣。
在沒有數位貨幣印表機的情況下,加密貨幣產業克服這一問題的一種方法是引入區塊鏈上可以給流動性供應商提供持續購買保證的資產。這些資產可能包括:大型股息生息股(為退休人員而被養老基金購買)、債券(為短期融資而被銀行和企業購買)、外匯(單個全球中心化法定貨幣很難實現,因此人民幣、美元、歐元等貨幣對仍將繼續使用)和商品(食物和取暖將始終有需求)。作為流動性供應商,在麥當勞 / 玉米這樣的交易對中提供流動性時,你會更加放心,因為你知道總會有一些需求,從而不會嚇跑流動性。即使出現偏離損失,作為流動性供應商,你也可以安心,因為你將成為一群快樂餐製造商或一群玉米的所有者。
附錄
關於冪律和為什麼加密貨幣和傳統金融將繼續存在這種現象:

一個很好的最近例子是(2023 年 1 月 8 日)共同演化的 DeFi 系統,其中 Curve 透過 Vyper 被攻擊,這反過來影響了其他協議如 Aave,進而影響了其他用戶對取款的決策。零日漏洞的存在導致該系統不斷演變,並處於失衡狀態,產生尾事件。
這是從網上獲取歷史資料的代碼:
import math
import numpy as np
import yfinance as yf #make sure to ‘pip install yfinance’
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#Download BTC/EUR as default
ticker1=”BTC-USD” #^GSPC, ^IXIC, CL=F,^OVX, GC=F, BTC-USD, JPY=X, EURUSD=X, ^TNX, TLT, SHY, ^VIX, LLY, XOM
ticker2=”EURUSD=X”
t_0=”2017-07-07″
t_f=”2023-07-07″
data1=yf.download(ticker1, start=t_0, end=t_f)
data2=yf.download(ticker2, start=t_0, end=t_f)
data3=data1
dat=data1[‘Close’]
dat = pd.to_numeric(dat, errors=’coerce’)
dat=dat.dropna()
dat_ret=dat.pct_change(1)
x = np.array(dat.values)
dat_recurrence=dat/max(dat)
xr = np.array(dat_recurrence.values)
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(6.5,3))
# Plot the logistic map in the first subplot
ax1.plot(range(len(x)), x, ‘#056398’, linewidth=.5)
ax1.set_xlabel(‘Time’)
ax1.set_ylabel(str(ticker1)+’/’+str(ticker2)+’ Price Ratio’)
ax1.set_title(str(ticker1)+’/’+str(ticker2)+’ Fluctuations since ‘+ str(t_0))
ax1.set_yscale(‘log’)
n_end=len(x)
# Create a recurrence plot of the logistic map in the second subplot
R = np.zeros((n_end, n_end))
for i in range(n_end):
for j in range(i, n_end):
if abs(xr[i] – xr[j]) < 0.01:
R[i, j] = 1
R[j, i] = 1
ax2.imshow(R, cmap=’viridis’, origin=’lower’, vmin=0, vmax=1)
ax2.set_xlabel(‘Time step’)
ax2.set_ylabel(‘Time step’)
ax2.set_title(‘Recurrence Plot of ‘ +str(ticker1)+’/’+str(ticker2))
series = pd.Series(dat_ret).fillna(0)
fig, ax = plt.subplots()
density = stats.gaussian_kde(series)
series.hist(ax=ax, bins=400, edgecolor=’black’,color=’#25a0e8′, linewidth=.2,figsize=(6.5,2),histtype=u’step’, density=True)
ax.set_xlabel(‘Log Returns’)
ax.set_ylabel(‘Log Frequency’)
ax.set_title(‘LogLog Histogram of Returns ‘ +str(ticker1)+’/’+str(ticker2))
ax.set_yscale(‘log’)
ax.set_xscale(‘log’)
ax.grid(None)
plt.scatter(series, density(series), c=’#25a0d8′, s=6)
fig, ax2 = plt.subplots()
series.hist(ax=ax2, bins=400, edgecolor=’black’,color=’#25a0e8′, linewidth=.2,figsize=(6.5,2),histtype=u’step’, density=True)
ax2.set_xlabel(‘Log Returns’)
ax2.set_ylabel(‘Log Frequency’)
ax2.set_title(‘Log-y Histogram of Returns ‘ +str(ticker1)+’/’+str(ticker2))
ax2.set_yscale(‘log’)
ax2.grid(None)
plt.scatter(series, density(series), c=’#25a0d8′, s=6)
plt.show()
雙曲線分佈和混合模型
import numpy as np
from matplotlib import pyplot as plt
from scipy import stats
p, a, b, loc, scale = 1, 1, 0, 0, 1
rnge=15
x = np.linspace(-rnge, rnge, 1000)
#Mixture model for tails
w=.999
dist1=stats.genhyperbolic.pdf(x, p, a, b, loc, scale)
dist2=stats.cauchy.pdf(x, loc, scale)
mixture=np.nansum((w*dist1,(1-w)*dist2),0)
plt.figure(figsize=(16,8))
plt.subplot(1, 2, 1)
plt.title(“Generalized Hyperbolic Distribution Log-Y”)
plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale), label = ‘GH(p=1, a=1, b=0, loc=0, scale=1)’, color=’black’)
plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘red’, alpha = .5, label=’GH(p=1, 0<a<1, b=0, loc=0, scale=1)’)
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘red’, alpha = 0.2) for a in np.linspace(1, 2, 10)]
plt.plot(x, stats.genhyperbolic.pdf(x, p,a,b,loc, scale),
color = ‘blue’, alpha = 0.2, label=’GH(p=1, a=1, -1<b<0, loc=0, scale=1)’)
plt.plot(x, stats.genhyperbolic.pdf(x, p,a,b,loc, scale),
color = ‘green’, alpha = 0.2, label=’GH(p=1, a=1, 0<b<1, loc=0, scale=1)’)
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘blue’, alpha = .2) for b in np.linspace(-10, 0, 100)]
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘green’, alpha = .2) for b in np.linspace(0, 10, 100)]
plt.plot(x, stats.norm.pdf(x, loc, scale), label = ‘N(loc=0, scale=1)’, color=’purple’, dashes=[3])
plt.plot(x, stats.laplace.pdf(x, loc, scale), label = ‘Laplace(loc=0, scale=1)’, color=’black’,dashes=[1])
plt.plot(x, mixture, label = ‘Cauchy(loc=0, scale=1)’, color=’blue’,dashes=[1])
plt.xlabel(‘Returns’)
plt.ylabel(‘Log Density’)
plt.ylim(1e-10, 1e0)
plt.yscale(‘log’)
x = np.linspace(0, 10000, 10000)
dist1=stats.genhyperbolic.pdf(x, p, a, b, loc, scale)
dist2=stats.cauchy.pdf(x, loc, scale)
mixture=np.nansum((w*dist1,(1-w)*dist2),0)
plt.subplot(1, 2, 2)
plt.title(“Generalized Hyperbolic Distribution Tail Log-Y Log-X”)
plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale), label = ‘GH(p=1, a=1, b=0, loc=0, scale=1)’, color=’black’)
plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘red’, alpha = .5, label=’GH(p=1, 0<a<1, b=0, loc=0, scale=1)’)
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘red’, alpha = 0.2) for a in np.linspace(1, 2, 10)]
plt.plot(x, stats.genhyperbolic.pdf(x, p,a,b,loc, scale),
color = ‘blue’, alpha = 0.2, label=’GH(p=1, a=1, -1<b<0, loc=0, scale=1)’)
plt.plot(x, stats.genhyperbolic.pdf(x, p,a,b,loc, scale),
color = ‘green’, alpha = 0.2, label=’GH(p=1, a=1, 0<b<1, loc=0, scale=1)’)
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘blue’, alpha = .2) for b in np.linspace(-10, 0, 100)]
[plt.plot(x, stats.genhyperbolic.pdf(x, p, a, b, loc, scale),
color = ‘green’, alpha = .2) for b in np.linspace(0, 10, 100)]
plt.plot(x, stats.norm.pdf(x, loc, scale), label = ‘Gaussian’, color=’purple’, dashes=[3])
plt.plot(x, stats.laplace.pdf(x, loc, scale), label = ‘Laplace(loc=0, scale=1)’, color=’black’,dashes=[1])
plt.plot(x, stats.cauchy.pdf(x, loc, scale), label = ‘Cauchy(loc=0, scale=1)’, color=’blue’,dashes=[1])
#Heavy tail mix model
plt.plot(x, mixture, label = ‘GH+Cauchy Mix(loc=0, scale=1)’, color=’red’,dashes=[1])
plt.xlabel(‘Log Returns’)
plt.ylabel(‘Log Density’)
plt.ylim(1e-10, 1e0)
plt.xlim(1e-0,1e4)
plt.xscale(‘log’)
plt.yscale(‘log’)
plt.legend(loc=”upper right”)
plt.subplots_adjust(right=1)
plt.show()
【免責聲明】市場有風險,投資需謹慎。本文不構成投資建議,用戶應考慮本文中的任何意見、觀點或結論是否符合其特定狀況。據此投資,責任自負。
*原文內容及圖片來源: Uniswap v3 数学洞察:数字资产的价格行为 – Foresight News
*封面圖片為AI生成之假想示意圖,生成出處網址: Pics for CW – Playground (playgroundai.com)












